数字化运营基础技能 – KMeans聚类分析实践案例

发表于： 2024年10月26日 2024年10月27日
标签： Python运营分析技能

K均值聚类
既然是聚类嘛，那肯定就用最经典也比较简单的K均值聚类方法。

K-Means算法是一种无监督的学习，事先不知道类别，自动将相似的对象归到同一个簇中。

也是一种聚类分析（cluster analysis）的算法，其主要是来计算数据聚集的算法，主要通过不断地取离聚类中心点最近均值的算法。

原理就不多说了，反正也都是用sklearn的包实现。

导入库

import matplotlib.pyplot as plt  # 图形库
import numpy as np
import pandas as pd
from sklearn.metrics import silhouette_score  # 导入轮廓系数指标
from sklearn.cluster import KMeans  # KMeans模块
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder  # 数据预处理库

读取数据

raw_data = pd.read_table('sales.txt', delimiter='\t')

数据预处理

# 缺失值审查
na_cols = raw_data.isnull().any(axis=0)  # 查看每一列是否具有缺失值
print('{:*^60}'.format('NA Cols:'))
print(na_cols[na_cols==True])  # 查看具有缺失值的列
print('Total number of NA lines is: {0}'.format(
    raw_data.isnull().any(axis=1).sum()))  # 查看具有缺失值的行总记录数

# 删除平均平均停留时间列
raw_data2 = raw_data.drop(['平均停留时间'], axis=1)

# 字符串分类onehotencode处理
cols = ['素材类型','广告类型','合作方式','广告尺寸','广告卖点']
model_ohe = OneHotEncoder(sparse=False)  # 建立OneHotEncode对象
ohe_matrix = model_ohe.fit_transform(raw_data2[cols])  # 直接转换
print(ohe_matrix[:2])

# 数据标准化
sacle_matrix = raw_data2.iloc[:, 1:7]  # 获得要转换的矩阵
model_scaler = MinMaxScaler()  # 建立MinMaxScaler模型对象
data_scaled = model_scaler.fit_transform(sacle_matrix)  # MinMaxScaler标准化处理
print(data_scaled.round(2))

# 合并所有维度
X = np.hstack((data_scaled, ohe_matrix))

KMeans建模

# 通过平均轮廓系数检验得到最佳KMeans聚类模型
score_list = list()  # 用来存储每个K下模型的平局轮廓系数
silhouette_int = -1  # 初始化的平均轮廓系数阀值
for n_clusters in range(2, 5):  # 遍历从2到5几个有限组
    model_kmeans = KMeans(n_clusters=n_clusters)  # 建立聚类模型对象
    labels_tmp = model_kmeans.fit_predict(X)  # 训练聚类模型
    silhouette_tmp = silhouette_score(X, labels_tmp)  # 得到每个K下的平均轮廓系数
    if silhouette_tmp > silhouette_int:  # 如果平均轮廓系数更高
        best_k = n_clusters  # 保存K将最好的K存储下来
        silhouette_int = silhouette_tmp  # 保存平均轮廓得分
        best_kmeans = model_kmeans  # 保存模型实例对象
        cluster_labels_k = labels_tmp  # 保存聚类标签
    score_list.append([n_clusters, silhouette_tmp])  # 将每次K及其得分追加到列表
print('{:*^60}'.format('K value and silhouette summary:'))
print(np.array(score_list))  # 打印输出所有K下的详细得分
print('Best K is:{0} with average silhouette of {1}'.format(best_k, silhouette_int))

聚类结果分析

# part1 将原始数据与聚类标签整合
cluster_labels = pd.DataFrame(cluster_labels_k, columns=['clusters'])  # 获得训练集下的标签信息
merge_data = pd.concat((raw_data2, cluster_labels), axis=1)  # 将原始处理过的数据跟聚类标签整合

# part2 计算每个聚类类别下的样本量和样本占比
clustering_count = pd.DataFrame(merge_data['渠道代号'].groupby(merge_data['clusters']).count()).T.rename({'渠道代号': 'counts'})  # 计算每个聚类类别的样本量
clustering_ratio = (clustering_count / len(merge_data)).round(2).rename({'counts': 'percentage'})  # 计算每个聚类类别的样本量占比

# part3 计算各个聚类类别内部最显著特征值
cluster_features = []  # 空列表，用于存储最终合并后的所有特征信息
for line in range(best_k):  # 读取每个类索引
    label_data = merge_data[merge_data['clusters'] == line]  # 获得特定类的数据

    part1_data = label_data.iloc[:, 1:7]  # 获得数值型数据特征
    part1_desc = part1_data.describe().round(3)  # 得到数值型特征的描述性统计信息
    # merge_data1 = part1_desc.iloc[2, :]  # 老版本，得到数值型特征的均值
    merge_data1 = part1_desc.iloc[1, :]  # 新版本，得到数值型特征的均值

    part2_data = label_data.iloc[:, 7:-1]  # 获得字符串型数据特征
    part2_desc = part2_data.describe(include='all')  # 获得字符串型数据特征的描述性统计信息
    merge_data2 = part2_desc.iloc[2, :]  # 获得字符串型数据特征的最频繁值

    merge_line = pd.concat((merge_data1, merge_data2), axis=0)  # 将数值型和字符串型典型特征沿行合并
    cluster_features.append(merge_line)  # 将每个类别下的数据特征追加到列表
# part4 输出完整的类别特征信息
cluster_pd = pd.DataFrame(cluster_features).T  # 将列表转化为矩阵
print('{:*^60}'.format('Detailed features for all clusters:'))
all_cluster_set = pd.concat((clustering_count, clustering_ratio, cluster_pd),axis=0)  # 将每个聚类类别的所有信息合并
print(all_cluster_set)

各类别显著数值特征对比

# part1 各类别数据预处理
num_sets = cluster_pd.iloc[:6, :].T.astype(np.float64)  # 获取要展示的数据
num_sets_max_min = model_scaler.fit_transform(num_sets)  # 获得标准化后的数据
# part2 画布基本设置
fig = plt.figure(figsize=(6,6))  # 建立画布
ax = fig.add_subplot(111, polar=True)  # 增加子网格，注意polar参数
labels = np.array(merge_data1.index)  # 设置要展示的数据标签
cor_list = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'w']  # 定义不同类别的颜色
angles = np.linspace(0, 2 * np.pi, len(labels), endpoint=False)  # 计算各个区间的角度
angles = np.concatenate((angles, [angles[0]]))  # 建立相同首尾字段以便于闭合
labels = np.concatenate((labels,[labels[0]]))   # 新版本增加，对labels进行封闭
# part3 画雷达图
for i in range(len(num_sets)):  # 循环每个类别
    data_tmp = num_sets_max_min[i, :]  # 获得对应类数据
    data = np.concatenate((data_tmp, [data_tmp[0]]))  # 建立相同首尾字段以便于闭合
    ax.plot(angles, data, 'o-', c=cor_list[i], label=i)  # 画线
# part4 设置图像显示格式
ax.set_thetagrids(angles * 180 / np.pi, labels, fontproperties="SimHei")  # 设置极坐标轴
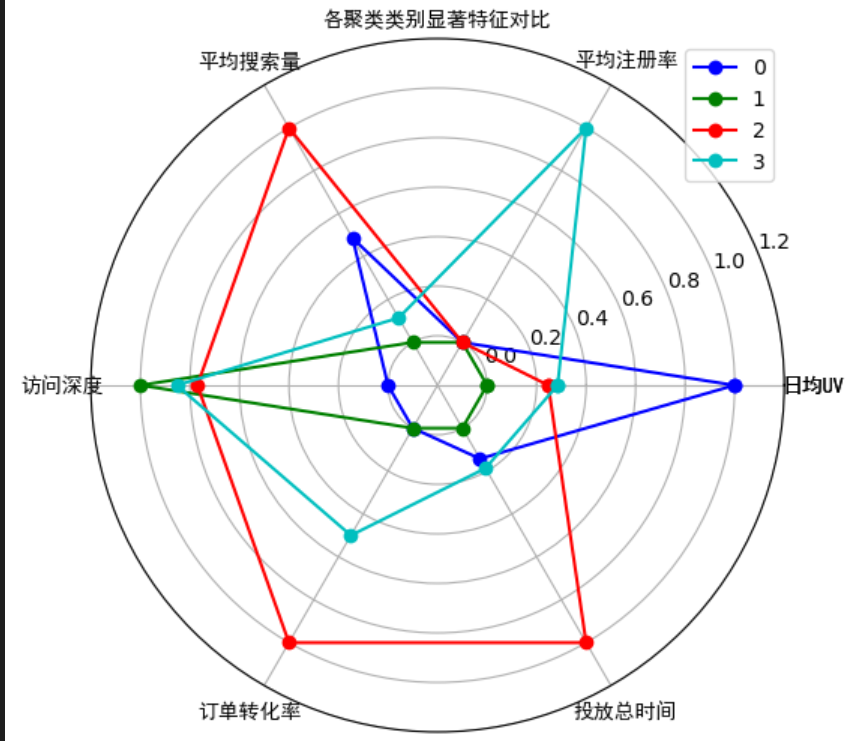
ax.set_title("各聚类类别显著特征对比", fontproperties="SimHei")  # 设置标题放置
ax.set_rlim(-0.2, 1.2)  # 设置坐标轴尺度范围
plt.legend(loc=0)  # 设置图例位置

viplao

332